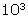You already know how to write numbers in two different ways, in decimal
and as a fraction. So you already know that 0.5 and 1/2 are the same
number represented or written in two different ways.
Since math is the universal language, math is used every day for
countless different reasons. Bankers and companies use decimal numbers
all the time for keeping track of money. Cooks use recipes that have
lots of fractions, like 1/4 cup of sugar for cookies. So decimal and
fractions are suitable for many purposes.
But scientists and engineers work with very large and very small
numbers all the time. The calculations that scientists and engineers
perform every day require greater precision or accuracy than two places
to the right of the decimal point that the rest of us use every day.
In order to be accurate in science and engineering, this often means
using many digits to the right of the decimal point.
Do you know how to calculate the circumference of a circle? Do you
remember the equation:
Circumference = 
x diameter
The symbol means the value
pi. Students usually use a simple value for pi, 3.14 or even 3.141.
But the real value of pi calculated to 50 decimal places is:
3.14159 26535 89793 23846 26433 83279 50288 41971
69399 37510
Now that's a hard number to work with!
But, what if you an engineer and you need precise calculations? Have
you heard of the Chunnel, the underwater tunnel that crosses the English
Channel and links Great Britain and France? The Chunnel is made of
interconnected cylinders. Don't you think that the engineers used
a highly accurate value for pi when they calculated the circumference
of each piece of the Chunnel?
But even for scientists and engineers, very large and very small
numbers are still hard to work with. So the numbers can be written
in different ways to make them easier to work with by looking at the
multipliers of 10 for large numbers and 0.1 for small numbers.
Writing numbers based upon powers of ten is called exponential notation.
Because exponential notation is used a great deal by scientists, it
is also called scientific notation. Exponential notation and scientific
notation are two names for the same thing.
Let's look at a sample large number used in science.
The speed of light is 30,000,000,000 cm/sec
Let's think about simplifying this number by dividing by 10. Every
time you divide by 10 you can eliminate a zero. So you could write
the speed of light as:
3.0 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10
x 10
That only made the number longer! But you know that 10 x 10 is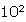 
so
10 10's multiplied together would be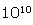 
.
Now we can write the speed of light in a simple way as
3.0 x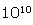
This works for any large number and is called exponential notation.
Exponential notation always has just one number to the left of the
decimal point. As an exercise, convert 5,678 to exponential. *
The same idea can be used for very small numbers. For example, the
mass of one hydrogen atom is
0.000000000000000000000001674 gram
In this case you divide the number by 0.1which 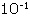is 
.
Count the zeroes to calculate the exponent you need. There are 23
zeroes so the equivalent value is
0.1674 x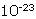 
While this is an accurate way to write the number, exponential notation
always has a number to the left of the decimal point. So the correct
exponential notation for
0.000000000000000000000001674 gram
is 1.674 x 
* Answer: 5.678 x 