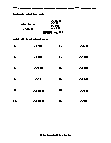Laws of Rational Exponents Worksheets
What are the Laws Rational Exponents? To solve mathematical problems with integers as exponents, you use specific rules. However, when it comes to problems that involve numbers with rational exponents, you can start freaking out. It may seem challenging, but if you take a deep breath, you will know that it is not that hard. Did you know that the rules for multiplying and dividing exponents also apply to rational exponents? Before we start learning the laws, you need to understand what rational exponents mean. a(1/n) = n √ a). am/n = n √ (am ) Zero-exponent Rule: anything raised to the power zero equals one. [a0=1] Power-Rule: you have to multiply the exponents when power is raising a power. [(a(1/m))(1/n) = a(1/mn) = mn √ a] Product Rule: When the same bases are multiplied with different exponents, you can simply add the exponents. [a(1/m) × a(1/n) =a(1/m+1/n)] Quotient Rule: When the same bases are being divided with different exponents, you can simply subtract the exponents. [a(1/m) ÷ a(1/n) = a(1/m-1/n)]
-
Basic Lesson
Demonstrates how imaginary numbers occur when a quadratic equation has no roots in the set of real numbers. An imaginary number occurs when a quadratic equation has no roots in the set of real numbers.
View worksheet -
Intermediate Lesson
Explores how to evaluate imaginary units in a binary system. Examples of pure imaginary numbers are 4i, √2i, etc.
View worksheet -
Independent Practice 1
Contains 20 Imaginary Unit problems. The answers can be found below. Solve the expression for x.
View worksheet -
Homework Worksheet
Imaginary Unit problems for students to work on at home. Example problems are provided and explained.
View worksheet -
Topic Quiz
What type of function is graphed below? A math scoring matrix is included.
View worksheet
Fun Fact
What inspired Einstein and his mathematical brilliance? It is reported that when a young Einstein was only five years old, his father gave him a compass to entertain him. Intrigued by the fact that whichever way he pointed the device the needle always pointed in the same direction, he began to wonder if there was some invisible force directly it. That simple childhood question turned into a lifelong mission as Einstein developed his masterful mind in the years to come.