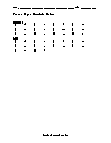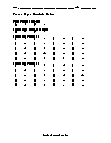Absolute Value Worksheets

What is Absolute Value? - In mathematics, an absolute term or commonly referred to as the modulus is denoted by |x| without any indication of the sign associated with it. The absolute value is a distance of a number from zero. For example, in the case below, the absolute value of 4 is 4. Yes, it may seem a bit obvious; why would not be the distance between 0 to 4 is 4. But absolute values show their true colors when the distance is not measured from 0. For example, the absolute value of -4 is also 4. The symbol for the absolute value is a | which is placed on each side of the number. For example, the absolute value of -6 is denoted by |-6|. It is important to remember that the absolute value for 5 and -5 is 5. So, it can be written as both |-5| or |5|. There is a wide range of applications where the generalization of absolute value takes place such as for quaternions, complex numbers, fields, ordered rings, and vector spaces.