Least Common Multiple Worksheets
What is the Least Common Multiple? Multiple is a number that, when divided, doesn't leave a remainder. For instance, 20 is a multiple of 5 or to put it another way, 5 x 4 = 20 and 20/5 = 4 Least Common Multiple or Lowest Common Multiple (LCM) of two integers is defined as the smallest positive integer divisible by both considered integers. This definition stands for all the non-zero integers. We can find the least common multiple by using different methods the most popularly used ones are: Repeated division, Prime factorization, Multiples. We demonstrate these each below.
-
Basic Lesson
Demonstrates how to find the least common multiple of number sets. Also includes practice problems.
View worksheet -
Intermediate Lesson
Asks students to find common multiples of 2 numbers. Find 3 Common Multiples of 2 and 3.
View worksheet -
Independent Practice 2
20 practice problems that review Least Common Multiple skills. The answers can be found below.
View worksheet -
Homework Worksheet
12 problems to reinforce the lessons and practice pages. An example is provided.
View worksheet
LCM by using repeated division
The given number is divided by the common divisor to a point no further division is possible by that common divisor. Once you reach this point, we multiply the divisors and the remainders together to get the product, which will be our LCM.
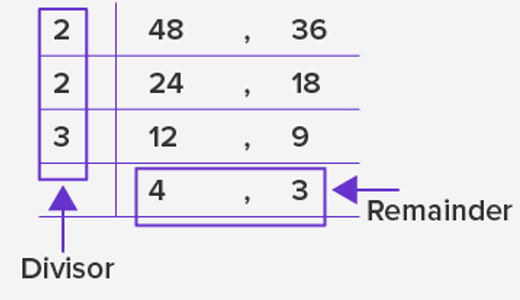
LCM = 2 x 2 x 3 x 4 x 3
LCM = 144
LCM by using prime factorization
We use a factorization tree of a given to generate a list of multiples. The very last branch of the factorization tree is referred to as the least common multiple of the given number. If we were to generate the factors of numbers 48 and 36 by using the factorization tree.
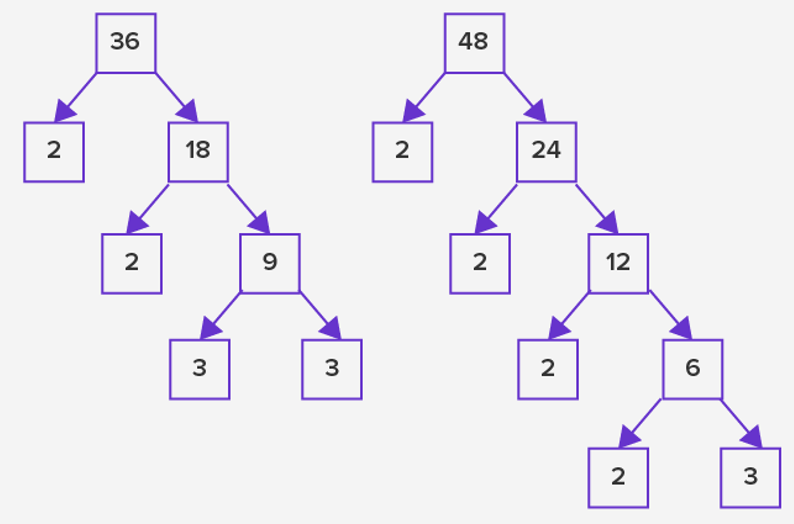
To figure out the prime factors of both the numbers, we would pair the common multiples.

LCM = 2 x 2 x 3 x 4 x 3
LCM = 144
LCM by using multiples
In this method, we would list the multiples of the given number. The first common multiples of a given number are the least common multiples. For numbers 36 and 48, 144 would be the least common multiple.
Separate Pieces
Factoring is like separating a number into pieces. It is expressing a number as the product of its factors. Factors are either composite numbers or prime numbers, except in the case of 1 or 0, which are neither. 1 is factor of all numbers.