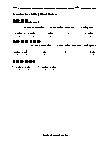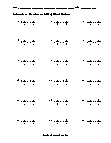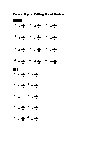Adding Mixed Numbers Worksheets

How to Add Mixed Numbers? A mixed number consists of both a fraction and a whole number. For example, 3 2/5 is the mixed number where 3 is the whole number, and 2/5 is the fraction. We can incorporate the following technique to add mixed numbers. Adding the Improper Fractions: The first technique includes five steps, which are described as follows: Convert the mixed numbers in the given problem into an improper fraction. For example, 13/4 will convert into 7/4 and 21/2 will convert into 5/2. The problem would become 15/5 + 5/2. Next, find the lowest common denominator of the two improper fractions. For the given problem we will have LCD = 4 The two improper fractions would have the same denominators. You will have 10/4 + 7/4. Add the converted fractions. 10/4 + 7/4 = 17/4. Now, write the improper fraction into a mixed number. You will get 4 1/4.