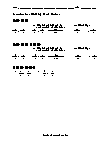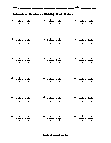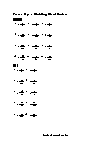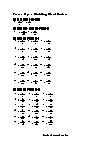Dividing Mixed Numbers Worksheets
How Do You Divide Mixed Numbers? When understanding the concept of fractions, we come across two different types. The first is the proper fractions and the second form are the improper fractions. Proper fractions are a case where the numerator is smaller than the denominator. In an improper fraction, the numerator is greater than the denominator. There are two ways of writing an improper fraction. The first is like a simple fraction a/b and then there are mixed numbers of the form C a/b. Applying arithmetic operations on simple fractions is simple, but students may freak out when they have to apply these operations on mixed numbers. So, how do we divide mixed numbers? Start by converting a mixed number into a fraction. How can you do that? Multiply the denominator with the whole number and then add the numerator. Place the result in the position of the numerator and the denominator will remain the same. Now, you will have two improper fractions with a division sign in between. You have to convert the division sign into multiplication, and this will result in the second number in the sum being reciprocated.
-
Basic Lesson
Demonstrates the division of mixed numbers. Includes practice problems. Convert mixed numbers into rational numbers. Division means multiplying by the inverse of the divisor. Multiply the numerators and multiply the denominators. Convert rational number into mixed number.
View worksheet -
Intermediate Lesson
Shows students step by step how to divide mixed numbers. 1. Convert mixed numbers into rational numbers. 2. Divide the numerators by the least common multiple of the denominators. 3. Simplify and convert the fraction to a mixed number.
View worksheet -
Independent Practice 1
Students divide a series of mixed numbers. The answers can be found below.
View worksheet -
Independent Practice 2
20 problems that review all skills within the unit. The answer key is below.
View worksheet -
Homework Worksheet
12 problems to reinforce the lessons and practice pages. An example is provided.
View worksheet -
Basic Lesson
Demonstrates the division of mixed numbers. Includes practice problems. 1. Multiply dividend by reciprocal of divisor. 2. Simplify.
View worksheet -
Independent Practice 1
Students divide a series of mixed numbers. The answers can be found below.
View worksheet -
Independent Practice 2
18 problems that review all skills within the unit. The answer key is below.
View worksheet -
Homework Worksheet
12 problems to reinforce the lessons and practice pages. An example is provided.
View worksheet
Actions
The only way I can distinguish proper from improper fractions is by their actions. Ogden Nash (1902-1971) American Poet, not to be confused with John Nash (1928-) American Mathematician, Nobel Prize winner & subject of "A Beautiful Mind."
In Word Problem Form
Al builds 32 models in a day; Sal can do the same in 3 days. If they work together, how long will it take them to build 32 models? Al works 3 times as fast, so he would be building 24 models; Sal does 8. Since 24 is 3/4 of 32, it would take 3/4 of a day.
How to Divide Mixed Numbers Refresher
A mixed number is a number that consists of a fraction and a whole number. For dividing mixed numbers, we first need to convert them into an improper fraction and then divide them like other fractions. Here we have enlisted a step-wise approach for dividing the mixed number. First, we need to multiply the denominator with the whole and add it with the numerator. For example, if we have 6 1/2 and 2 1/4 , you will multiply 6 x 2 + 1 = 13 and 2 x 4 +1 = 9. The obtained fraction will be 13/2 and 9/4. These two fractions are improper fractions that will be used for division. The sum we will get will be 13/2 ÷ 9/4. Next, we will take the reciprocal of the second fraction. So, the numerator will become the denominator, and the denominator will become the numerator. In this example, 9/4 will become 4/9. Also, when we take the reciprocal, the division sign will change into a multiplication sign. The sum will look like, 13/2 x 4/9. Multiply the numerators, 13 x 4 = 52 and the denominators 2 x 9 = 18. The fraction we will get will be: 52/18. Simplify the answer, if possible. In our example, the answer is divisible by 2. Simplifying the answer with 2, we will get, 26/9. Write the improper fraction in mixed form. Our answer will be, 2 8/9.