Dilations Worksheets
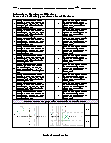
What are Dilation Transformations? In mathematics, a dilation is a function from a metric space into itself that satisfies the identity for all points, where is the distance from to and is some positive real number. In Euclidean space, such a dilation is a similarity of the space. Dilations change the size but not the shape of an object or figure. OR A dilation is a transformation that produces an image that is the same shape as the original, but is a different size... A description of a dilation includes the scale factor (or ratio) and the center of the dilation. The center of dilation is a fixed point in the plane.
-
Basic Lesson
Guides students through recognizing dilations. Under a dilation, triangle A(0,0), B(0,2), C(4,0) becomes triangle A'(0,0), B'(0,4), C(8,0). What is the scale factor for this dilation? B(0,2) becomes after dilation B'(0,4) that means y coordinate changed 2 to 4.
View worksheet -
Intermediate Lesson
Demonstrates the use of coordinates with dilations. Triangle ABC becomes A'B'C' after dilation as shown in figure. What is the scale factor?
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concepts of the Dilations.
View worksheet -
Independent Practice 2
Students use Dilations in 20 assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with 12 problems to achieve the concepts of Dilations.
View worksheet -
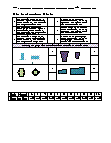
Basic Lesson
Guides students through solving transformations in the form ofg dilations. If an image is 7 units in size, under a dilation of scale factor 3 what will be the size of figure after dilation?
View worksheet -
Intermediate Lesson
Demonstrates the concept of advanced skill while solving these problems. Under a dilation, the picture shown at the left has been reduced in size just half of the image. What is the scalar factor.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concepts of the core skill that is lead here. The length of a pencil is 6 inches. Under a dilation of scale factor 2, the length of the large/small pencil is:?
View worksheet -
Independent Practice 2
Students work on 20 different assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with 12 problems to achieve the concepts we explored.
View worksheet
Question: Where did Christopher Complementary begin his journey?
Answer: At the Verta Seas.