Transformations Worksheets
What are Geometric Transformations? The geometric transformation includes taking a preimage and molding or transforming it to obtain an image. Broadly, there are two types of geometric transformations: The non-rigid transformation that alters the size of the preimage while keeping the shape intact. The rigid transformation doesn't alter the size or shape of the preimage. Types of Transformation - Rigid and non-rigid transformations are further divided into different categories. Rotation, translation, and reflection fall in the rigid transformation, and dilation fall in the non-rigid category. Below we have briefly discussed each sub-category. Translation - It is a type of transformation that slides or moves across the plane or through space. In translation, all points of a figure move or slide in the same direction and cover the same distance. Rotation - As the name implies, rotation moves the figure about a line or point. It basically means to spin or turn the figure at a point. The point of turning or spinning is known as the center of rotation. This center can lie outside the figure or be present on the figure. Reflection - Reflection is a transformation that involves flipping the shape across the line to create a mirror image, in the mirror image, the measures of lines and angles are preserved. Dilation - Dilation is the transformation that involves expanding or contracting the shape without disturbing its orientation or shape.
-
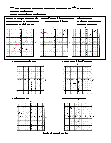
Basic Lesson
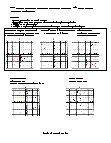
Guides students through the concept of transformations. Label the figure with the correct term. Translation (slide), Rotation (turn), Reflection (flip).
View worksheet -
Intermediate Lesson
Demonstrates how to identify a translation, rotation, or reflection.
View worksheet -
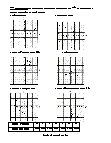
Independent Practice 1
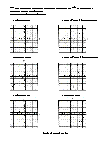
Students determine is the transformation taking place is a translation, rotation, or reflection.
View worksheet -
Independent Practice 2
Students determine the type of transformation in 20 assorted problems. The answers can be found below.
View worksheet -
Basic Lesson
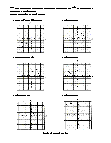
Demonstrates translations, rotations, and reflections with great detail. Draw the triangle after the transformations. A translation is a slide where the figure is moved either horizontally or vertically or both. A rotation is a turn around a point. A reflection is a flip of the figure over a line. The transformed figure is the mirror image of the original.
View worksheet -
Independent Practice 1
6 draw the triangle after the transformation problems. The answers can be found below. Draw the triangles after the transformations.
View worksheet -
Basic Lesson
Guides students through identifying translations from a variety of choices. A translation moves an object without changing its size or shape and without turning it or flipping it. The translation of an object is called its image.
View worksheet -
Intermediate Lesson
Demonstrates how to describe and apply translations. Describe the translation as horizontal of Vertical for the figures above. The object is flipped horizontally (left to right).
View worksheet -
Independent Practice 1
A really great activity for allowing students to reinforce the concept of Working with Translations.
View worksheet -
Independent Practice 2
Students Work with Translations in assorted problems. The answers can be found below.
View worksheet -
Independent Practice 3
An in-depth review of Working with Translations are found on this worksheet .
View worksheet -
Independent Practice 4
Students draw on past knowledge to solve this set of Working with Translations problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Working with Translations.
View worksheet
Geometry Poem and Joke
Roses are red,
Violets are blue,
Greens' functions are boring
And so are Fourier transforms.
Want a quick problem solving tip? Here's one: The only angle
from which to approach a problem is the try-angle!