Triangle Proofs Worksheets

What Are Triangle Proofs? Recall that triangles have three sides and are a construct of three points or vertices. Where any three points can come together to form a triangle, any three lines cannot come together to form a triangle. But in order to prove this, we need some logic and theorems. Let us consider the fact that the sum of all the interior angles of a triangle is 180 degrees. We all know that this fact is true, but let us understand how this is proven to be true. Triangle Sum Theorem - Consider a triangle ABC:

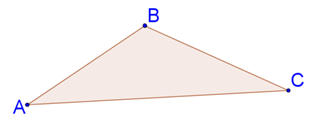
Take this triangle and draw a parallel line opposite to the side AC through vertex B.

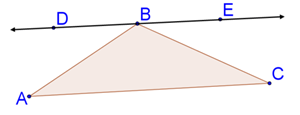
We know that alternate interior angles are congruent when lines are parallel. Considering this fact, we know that ∢A is congruent to ∢DBA, hence ∢A=∢DBA. Similarly, ∢C and ∢EBC are alternate interior angles showing congruence with each other, hence ∢C=∢EBC. If we observe the diagram shown above, we can see that ∢EBC, ∢ABC, ∢DBA form a straight line. Therefore, ∢EBC+ ∢ABC+ ∢DBA = 180 degrees. Hence, the statement "the sum of the measures of the interior angles of a triangle is 180 degrees" is proven. You can use this theorem to solve other geometrical problems.