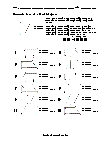Area of a Parallelogram Worksheets
How to Find the Area of a Parallelogram - Any shape that has the word parallel in it explicitly tells the reader or the viewer that the shape has two opposite pair of parallel sides. A parallelogram is a two-dimensional, closed figure with straight sides. It seems like a quadrilateral, which is a four-sided shape. Because the parallelogram has its opposite sides parallel, the angles that are formed at these parallel lines are also congruent. Examples of parallelogram includes a rhombus, three quadrilaterals, a square, and a rectangle. These are the specific types of parallelograms. If you take notice of these parallelograms, you will notice that all of these have length, base, and height. Perhaps, you know the basic protocol of finding the area of the parallelogram, which involves the use of all three measures. The formula to find the area of a parallelogram is : Base x Height. All you have to do is out in the values of the base and height of the parallelogram, and you will have the answer.
-
Basic Lesson
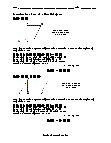
Guides students through finding the area of a parallelogram by using a corner. Find the area of a parallelogram with a base of 7 cm and corresponding height of 6 cm.
View worksheet -
Intermediate Lesson
Demonstrates how to break a parallelogram into many parts. Find the area of a parallelogram with a base of 24 cm and corresponding height of 14 cm.
View worksheet -
Independent Practice 1
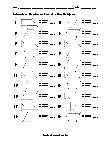
A really great activity for allowing students to understand the concepts of the area of a Parallelogram.
View worksheet -
Independent Practice 2
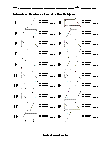
Students determine the area of a parallelogram in 20 assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with 12 problems to achieve the concepts of Area of a Parallelogram.
View worksheet
The Battle
3 kingdoms waged a battle. 2 of the groups had over 50 squires each, the other had only1. All sides readied, with the lone squire hanging a pot from a rope in a tree. In the end, the lone squire won, proving the squire of the high pot & noose is equal to the squires of the other 2 sides.