Truth Tables for Biconditionals Worksheets

What Are the Trends of Truth Tables for Biconditionals? In mathematical logic, every statement is either true or false. The logical biconditional statement is also called material biconditional. It logically joins the two statements p and q. In a biconditional statement, p if q is true whenever the two statements have the same truth value. Otherwise, it is false. It is denoted as p ↔ q. In other words, logical statement p ↔ q implies that p and q are logically equivalent. A logic involves the connection of two statements.

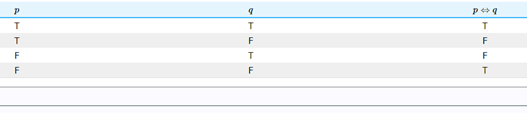
For better understanding, you can have a look at the truth table above. A logic statement is true if both the statements carry the same meaning. It is true either when bot the statements are true, or both are false. Otherwise, it is false.