Truth Tables for Conditionals Worksheets

What Are the Trends of Truth Tables for Conditionals? The basics of mathematical logic goes with the if and is conditional statements. A conditional statement, symbolized by p → q, is an if-then statement in which p is a hypothesis and q is a conclusion. The logical connector in a conditional statement is denoted by the symbol →. The conditional is defined to be true unless a true hypothesis leads to a false conclusion. The table for truth statements goes as follows: 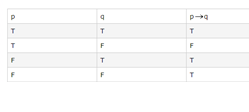In the truth table above, p → q is only false when the hypothesis (p) is true, and the conclusion (q) is false; otherwise, it is true. It means there are more chances for a statement to be true then to be false. If a true hypothesis leads to a false conclusion, then the conditional statement is considered true. Note: A conditional statement is a compound statement.