Determinants of a Matrix Worksheets
How Do You Calculate the Determinant of a Matrix?
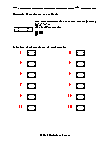
By definition, the determinant is a scaler value of any squared matrix, which tells us the properties of the linear transformation. However, to find the determinant value of any 2 x 2 matrix, you can simply multiply the first and third element of matrix and subtract it with the product pf the second and fourth element in it. Let’s take a look at the example below.
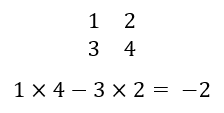
However, if you want to find out the determinant of 3 x 3 matrix, then the number of steps somewhat change. Let's look at the following example.
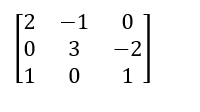
Expanding by C1,
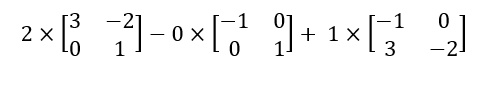
If we look back to what we did, we can see that we expanded by 1st column and placed an imaginary pointer on its every element. In the middle of it, we neglected all elements in front, above, and below it. We also added a minus sign before the second element. Now, we will resolve the 2x2 matrices with the same method as mentioned above.
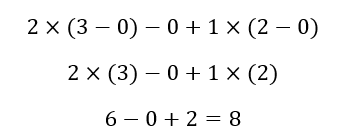
-
Independent Practice 1
A really great activity for allowing students to understand the concept of Determinants 2x2 Matrix. Calculate the determinant of each matrix.
View worksheet -
Independent Practice 2
Students find the Determinants 2x2 Matrix in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Determinants 2x2 Matrix.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of Determinants 3x3 Matrix.
View worksheet -
Independent Practice 2
Students find the Determinants 3x3 Matrix in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Determinants 3x3 Matrix.
View worksheet -
Basic Lesson
Guides students through solving determinants with the diagonal method. In diagonal method of solving determinants all the elements of the determinant are made zero, except the diagonal elements.
View worksheet -
Intermediate Lesson
Demonstrates how to treat diagonal elements within a matrices. The elements are made zero by adding rows or columns; subtracting rows or columns; multiplying or dividing whole row or column by a scalar.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of 3x3 Matrix Diagonals.
View worksheet -
Independent Practice 2
Students find the 3x3 Matrix Diagonals in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of 3x3 Matrix Diagonals.
View worksheet
National Metric Day?
Did you know that the United States government has slated October 10th as National Metric Day each year? That's amazing since no one in the U.S. really even uses the Metric System!