A mathematician, scientist, and engineer are each asked: "Suppose we define a horse's tail to be a leg. How many legs does a horse have?" The mathematician answers "5"; the scientist "1"; and the engineer says "But you can't do that!

Home > Math Skills / Topics > Matrices Worksheets > Subtraction of Matrices Worksheets

Subtraction of Matrices Worksheets

Free Math Worksheet = free Member Math Worksheet = members only

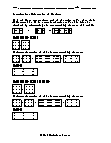
Basic Lesson: Guides students through determining the difference between matrices.; Standard: MATH 3
Grades: (9-12); View lesson

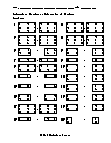
Intermediate Lesson: Demonstrates a step-by-step method for working subtracting matrices.; Standard: MATH 3
Grades: (9-12); View lesson

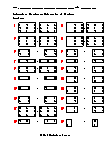
Independent Practice 1: A really great activity for allowing students to understand the concept of Subtraction of Matrices .; Standard: MATH 3
Grades: (9-12); View worksheet

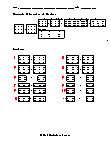
Independent Practice 2: Students find the Subtraction of Matrices in assorted problems. The answers can be found below.; Standard: MATH 3
Grades: (9-12); View worksheet

Subtraction of Matrices Homework: Students are provided with problems to achieve the concepts of Subtraction of Matrices.; Standard: MATH 3
Grades: (9-12); View homework

Subtraction of Matrices Quiz: This tests the students ability to evaluate Subtraction of Matrices.; Standard: MATH 3
Grades: (9-12); View quiz

Answer Keys: Answers for the homework and quiz.; View answers

Answer Keys: Answers for lessons and both practice sheets.; View answers

How to Reduce Anxiety and Nervousness on Math Tests: Sweaty palms, dry mouth, heart palpitations and to top it all up, your mind goes totally blank instantly.; View Math Article

Why getting the correct math answer is not always important.: Clearly, showing one's work provides an insight into where problem areas may lie.; View Math Article

More Advanced Math Worksheets

More Advanced Worksheets: The next level of math skills.; -Complex Number Operations
-Applied Inequalities
-Express Logarithms
-Polynomial Word Problems

Less Advanced Math Worksheets

Remedial Math Worksheets: Skills needed to get to this level.; -Algebraic Translations
-Categorizing Data and Bias
-Combinations
-Like Terms