Law of Sines Worksheets

What is the Law of Sines? In the world of trigonometry, there is another law that is used to determine the nature of a triangle, i.e., the law of sines. The law of sines is considered as the relationship between the sides and the oblique angles of the triangles. In other words, it simply states that the ratio of the length of any side of a triangle and the sine of the opposite angle remains the same for all sides of the triangle. 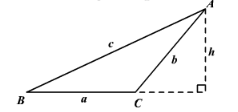In retrospect, for a triangle ABC which is oblique with the sides a, b, and c, the law of sines will be:

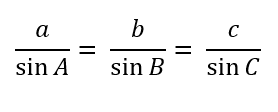
To use the Law of Sines, you need to know either two angles and one side of the triangle (AAS or ASA) or two sides and an angle opposite one of them (SSA).