Rational Expressions Operations Worksheets
What Are Rational Expressions Operations?
The rational expressions are the one with a fraction containing the numerator or denominator in the form of a polynomial. It can be both, i.e., the numerator or the denominator or either one in the form of a polynomial.
For example;
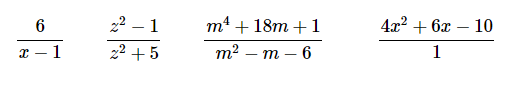
Here the point to ponder is the last expression. It is usually written as the simple expression 4x2 + 6x - 10 = 0, but the need is to understand that such polynomials can also be considered as rational expressions. As a rule, goes by, the division with zero is not possible. This is applicable to rational expressions as well. The division with zero is not possible in any case.
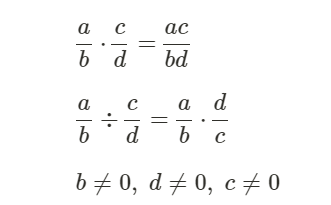
The addition and subtraction of the rational numbers are a bit trickier, and we need to be careful while solving these. For this, we begin with finding common denominators while finding equal fractions.
-
Basic Lesson
Guides students solving equations that involve an Rational Expressions Operations. Demonstrates answer checking. For addition of rational numbers make the denominator of the terms same and then add as numerical expressions. The Denominator of 1st term is 2, either take L.C.D of both denominator or multiply the 1st term by 2.
View worksheet -
Intermediate Lesson
Demonstrates how to solve more difficult problems. For subtraction of rational numbers make the denominator of the terms same and then add as numerical expressions. Take L.C.D.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of Rational Expressions Operations. Simplify in the simplest form.
View worksheet -
Independent Practice 2
Students find the Rational Expressions Operations in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Rational Expressions Operations.
View worksheet -
Skill Quiz
This tests the students ability to evaluate Rational Expressions Operations.
View worksheet
Isaac Asimov Quote
"After years of finding mathematics easy, I finally reached integral calculus and came up against a barrier. I realized that this was as far as I could go, and to this day I have never successfully gone beyond it in any but the most superficial way."