Angle Sums and Differences Worksheets
How to Determine the Sum of Differences with Angles -
Finding out the value of the trigonometric identities can be much easier if we use the concept of sum and differences of identities. In other words, it is way tougher to find out the value of sin15, but if we apply a difference identity of the sine function, then it becomes much easier. Like, if we find out the value of sin (45-30). However, you cannot just write sine 45 and sine 30 separately and subtract them. So, let us discuss the formula in detail.
The difference formula for the sine function is sin(α- β) = sinα cosβ - cosα sinβ. In this scenario, α is 45°, while β is 35°. Now, let us solve the problem.
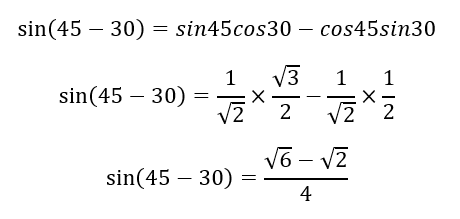
Similarly, there are other formulae as well, i.e., sum identity of sine, and both sum and difference identity of cos.
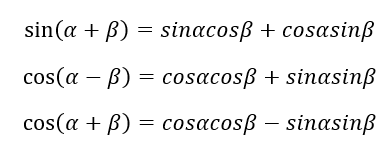
-
Basic Lesson
Guides students solving equations that involve an Angle Sums & Differences Demonstrates answer checking. The positive square root is chosen because Cos 15° lies in Quadrant I. The positive square root is chosen because Cos 5° lies in Quadrant I.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of Angle Sums & Differences.
View worksheet -
Independent Practice 2
Students find the Angle Sums & Differences in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Angle Sums & Differences.
View worksheet
S. Gudder Quote
The essence of mathematics is not to make simple things complicated, but to make complicated things simple.