Transformations with Functions Worksheets

What is a Function Transformation? The transformation of functions is used to represent the functions in the form of a graph. It is as simple to understand as that. First, we need to understand what are the functions. A function represents the relation If you start with a simple parent function y=f(x)y=f(x) and its graph, certain modifications of the function will result in easily predictable changes to the graph. For example:Horizontal Shift - Replacing f(x) with f(x−b) results in the graph being shifted b units to the right between two or more values.

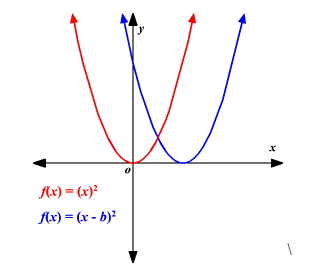
Here are the important notes to keep in mind while using the function transformation. There is a vertical shift in the function if we add a constant to the output. There is a horizontal shift in the function if we add a constant to the input. We need to thoroughly examine the additions on the input or output side to compare and interpret vertical and horizontal shifts. Vertical and horizontal shifts often occur simultaneously.