Special Right Triangles Worksheets
What Are Special Right Triangles? We know that there are equilateral triangles with all equal sides and angles. We have an isosceles triangle with two equal sides and two equal angles, we have scalenes with no equal sides or angles, and right-angled triangles that have one 90° angle and three unequal sides. But what are special right triangles? There are two types of special right triangles; the first one is 30-60-90 triangles and 45-45-90 triangles. The first one is a triangle with 30° and 60° as its acute angles. The sides of these triangles have special proportions. The base is half of the hypotenuse length, and the height is √3/2 times of the hypotenuse length. The type 2 special triangles have 45° acute angles. Here the base and the height are equal, and the hypotenuse is √2 times of that height.
-
Basic Lesson
Guides students solving equations that involve an Special Right Triangles. Demonstrates answer checking.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of Special Right Triangles.
View worksheet -
Independent Practice 2
Students find the Special Right Triangles in assorted problems. The answers can be found below. What is the measure of angle AEB?
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Special Right Triangles.
View worksheet -
Basic Lesson
Guides students solving equations that involve an Special Right Triangles. Demonstrates answer checking.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of Special Right Triangles.
View worksheet -
Independent Practice 2
Students find the Special Right Triangles in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of Special Right Triangles.
View worksheet -
Basic Lesson
Guides students solving problems that involve an working with right triangles. Demonstrates answer checking. A ladder leans against a building. The foot of the ladder is 6 feet from the building. The ladder reaches a height of 14 feet on the building. Find the length of the ladder to the nearest foot.
View worksheet -
Intermediate Lesson
Demonstrates how to solve more difficult problems. From a point on the ground 25 feet from the foot of a tree, the angle of elevation of the top of the tree is 32 degrees. Find to the nearest foot, the height of the tree.
View worksheet -
Independent Practice 1
A really great activity for allowing students to understand the concept of working with right triangles. A Bamboo leans against a wall. The foot of the bamboo is 10 feet from the wall. The ladder reaches a height of 15 feet on the wall. Find the length of the bamboo?
View worksheet -
Independent Practice 2
Students start working with right triangles in assorted problems. The answers can be found below.
View worksheet -
Homework Worksheet
Students are provided with problems to achieve the concepts of working with right triangles.
View worksheet
How to Find Measures of Right Triangles
Right triangles are those triangles in which one of the sides has an angle of 90o. However, learning to find the measures of a right-angled triangle can be quite simple. Firstly, we need to find the lengths of two of its sides. But the question is which one to use?
The first step is to find the names of the two sides given. Let us take an example.
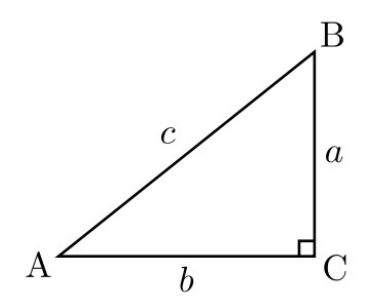
Now, in this scenario, the c side is the hypotenuse since its in front of the right angle. Now, b is the side adjacent to the angle and front of it is which is the opposite side. The next step is to learn which of the sides are given. Remember, you need to know the values of at least 2 sides. Imagine, you know the sides hypotenuse and opposite, and then you can use the following property.
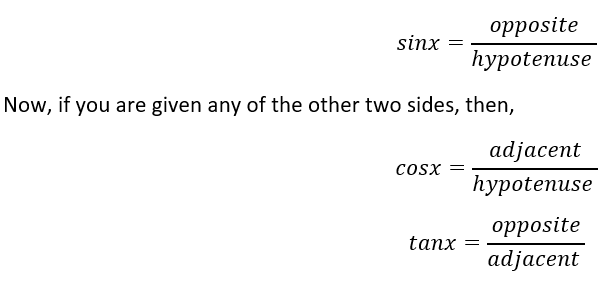
A Contest...
A student comes to the department with a shiny new cup, the sort of which you get when having won something. He explained: I won it in the MD Math Contest. They asked what 7 + 7 is. I said 12 and got 3rd place!




















