What is the Deal with PEMDAS?: Order of Operations


Article Summary: There order operations needs to be completely understood by you, because when you move into Algebra knowing the order of operations is critical. PEMDAS was developed as a mnemonic that was designed to help you remember the order of operations. A recommendation is to write PEMDAS on your problem sheets when work the problems so that you can learn to integrate it into your logical mathematical skills.

So what is the deal with PEMDAS? It is called the order of operations, but why the PEMDAS acronym? This acronym stands for Parenthesis, Exponents, Multiplication, Division, Addition, and Subtraction. It is typically remembered by using the mnemonic "Please Excuse My Dear Aunt Sallie." The order of operations is used for every math problem. All math problems are designed to find answers using different ways to solve the problem. However, they all follow the order of operations.

Let's take a look at simple problem: a( b + c - d )

The first thing you do is look at PEMDAS at determine which gets answered first. Sine we read from left to right we will solve for parenthesis first. Then try to solve for exponents, there is nothing to solve because there are no exponents. Next try to solve for Multiplication, however we need to solve the inside the parentheses first.

Let's plug in some numbers: 2( 3 + 6 - 1 )

Using the method described above it would be 2(3 + 6 - 1) = 2(9 - 1) = 2(8) = 16 or it can be solved this way 2(3 + 6 - 1) = 2(3 + 5) = 2(8) = 16. Either way you will come out with the same answer because it does not matter which you do first Addition or Subtraction.

Many students will try to solve it this way 2(3 + 6 - 1) = 2 x 3 + 6 - 1 = 6 + 6 - 1 = 12 - 1 = 11 (which is incorrect). This is caused by trying to follow the left to right operations typical of many problems that do not have parentheses. Anytime you see parentheses in a problem solve everything inside the parentheses first.

Let's try one with exponents:

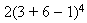
using PEMDAS. First we solve everything inside parentheses, followed by exponents, and then multiplication.

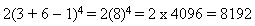
Following the order operations or PEMDAS is a critical step that must be completed in every math problem once an expression can be written. Even when completing written problems, you need to always determine the expression that is derived from the story and use PEMDAS to complete the problem.

Lets take another look at order operations using are more challenging problem, see if you can pick out each step that follows the PEMDAS model.

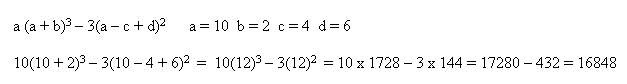
Let's look at another problem and explain it a different way:

3 (2 + 5) + 5 (2 + 6) / 4 The Problem
3(7) + 5(8) / 4 Parentheses - addition
21 + 40 / 4 Multiplication
21 + 10 Division
31 Addition

As you can see there is really nothing mystical or complicated when solving a problem when using PEMDAS - Order of Operations. It does not so let's try another expression:

3(5 + 6) + 4(4 + 3) / 3 + 6 - 12 The Problem
3(11) + 4 (7) / 3 + 6 - 12 Parentheses - addition
33 + 28 / 3 + 6 - 12 Multiplication
33 + 9.33 + 6 - 12 Division
48.33 - 12 Addition
36.33 Subtraction

There order operations needs to be completely understood by you, because when you move into Algebra knowing the order of operations is critical. PEMDAS was developed as a mnemonic that was designed to help you remember the order of operations. A recommendation is to write PEMDAS on your problem sheets when work the problems so that you can learn to integrate it into your logical mathematical skills.